Note: 以下虽然将预测结果称为概率,但其本身并不具有概率的内在含义,其本质上只是各个类别的得分情况。
cross entropy系列
- 把每个像素看作一个单独的sample
- 整个图像的loss是所有像素loss的(加权)平均值
- 实际使用中,可以用weighted focal loss:$\text{pixel loss}=-\sum\limits_{classes}\alpha_{class}(1-y_{pred})^\gamma \times y_{true}log(y_{pred})$,以同时解决难学习样本问题和样本数量不均衡问题
basic CE loss
- cross entropy loss (ce loss)
- 适用于二分类及多分类问题
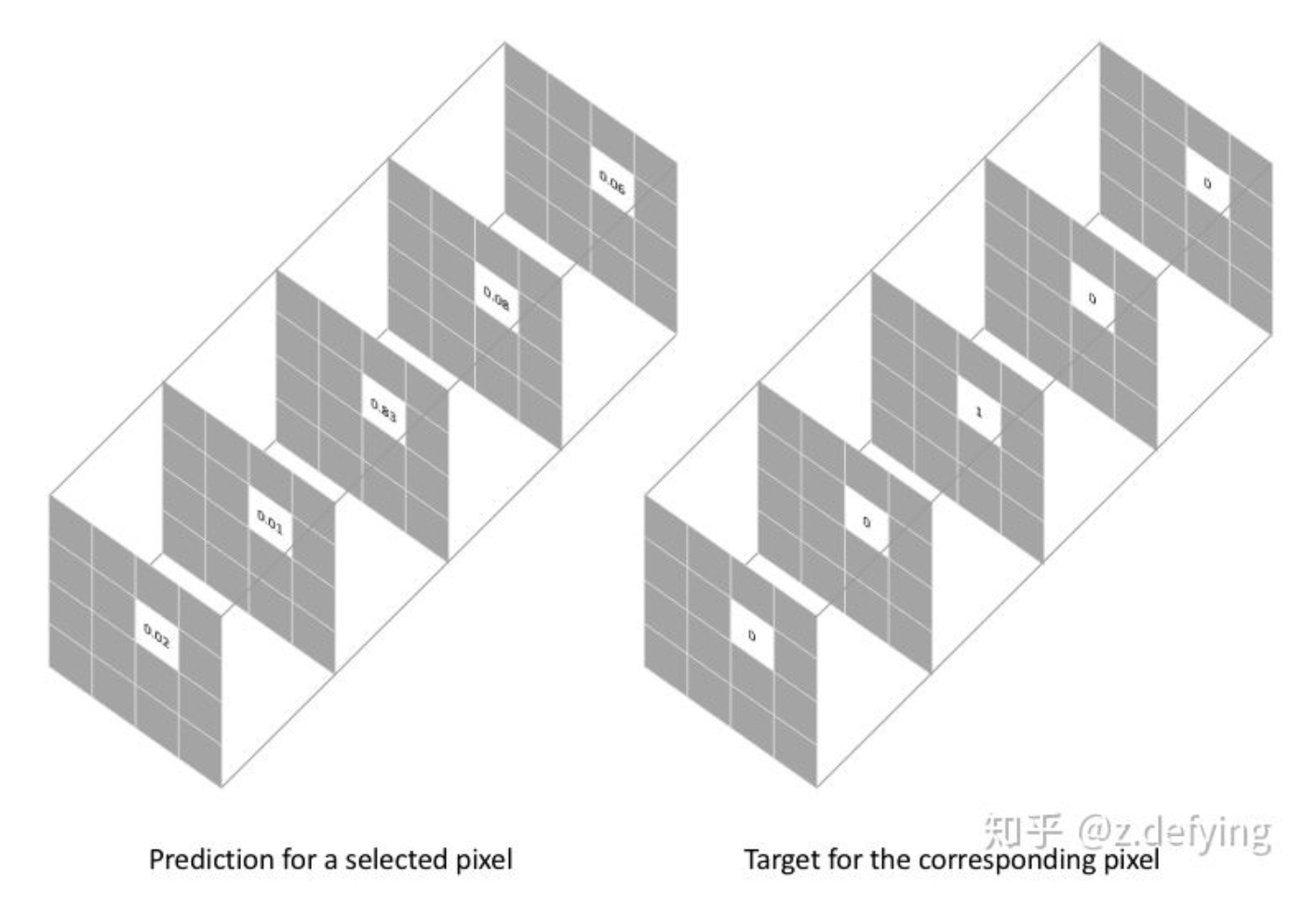
- 用多通道one-hot标签表示ground-truth。prediction同样为多通道,每个通道表示属于各个类的概率
- 用一个像素的预测结果(概率分布向量)和它的one-hot标签向量比较,得到该像素的损失:$\text{pixel loss}=-\sum\limits_{classes}y_{true}log(y_{pred})=-log(y_{\text{true_pred}})$。化简后的结果就是该像素的真实类别所对应的预测值的负log值。
- binary cross entropy loss (bce loss)
- 适用于二分类问题
- 单通道图表示ground truth,0为负样本,1为正样本。prediction同样为单通道,表示为1(正样本)的概率
- 每个像素的损失为:$\text{bce loss}=-y_{true}log(y_{pred})-(1-y_{true})log(1-y_{pred})$
weighed CE loss
- 针对在图像中多个类的样本不均衡问题。基本的交叉熵损失为各个像素损失的平均值,也就是平等的对待各个像素(样本)。此时如果多个类的样本数量分布不均衡,图像最终的损失将由样本数量多的类别对应的损失所主导,导致模型会主要学习样本数量多的类别的特征,并且学习出来的模型会更偏向将像素预测为该类别。
- 为了避免图像最终的损失由样本数量多的类别对应的损失所主导,可以选择增大样本数量少的类的损失,即为不同样本数量的类别对应的损失添加不同的权重
- 加权交叉熵损失函数:$\text{pixel loss}=-\sum\limits_{classes}\alpha_{class}\times y_{true}log(y_{pred})$,其中 $\alpha_{class}$ 对应不同类别的权重
focal loss
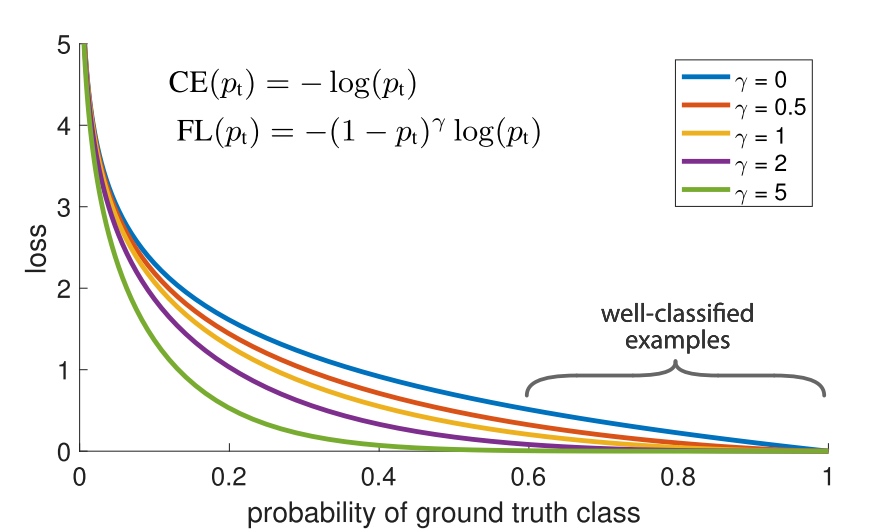
- 使网络更加关注难学习样本。当图像中存在大量的易学习像素(对应类别的 $y_{pred}>0.5$)和少量的难学习像素(对应类别的 $y_{pred}<0.5$)时,虽然易学习像素的loss小于难学习像素的loss,但由于样本数量的影响,大量易学习像素总体的loss也将远远超过少量难学习像素总体的loss,使得图像最终的loss由大量易学习像素的loss所主导,导致模型趋向于继续关注大量易学习的样本,而不会关注难学习的样本。
- focal loss修改交叉熵损失函数为:$\text{pixel loss}=-\sum\limits_{classes}(1-y_{pred})^\gamma \times y_{true}log(y_{pred})$,其中 $y_{pred}$ 越小(越难学习),对应的权重越大。实验表明 $\gamma=2$ 效果最好。
- focal loss也一定程度上解决了样本数量不平衡问题。因为样本数量少的类别对应的像素往往也是难学习的像素,因此关注难学习样本有助于关注样本数量少的类别。
dice loss系列
待填…