Take away message
- 出发点:The depth of representations is of central importance for many visual recognition tasks.
- 问题:Deeper networks have degradation problems.
- 解决方案:We explicitly reformulate the layers as learning residual functions with reference to the layer inputs, instead of learning unreferenced functions. Experiments show that these residual networks are easier to optimize, and can gain accuracy from considerably increased depth.
Degradation problem of deeper network
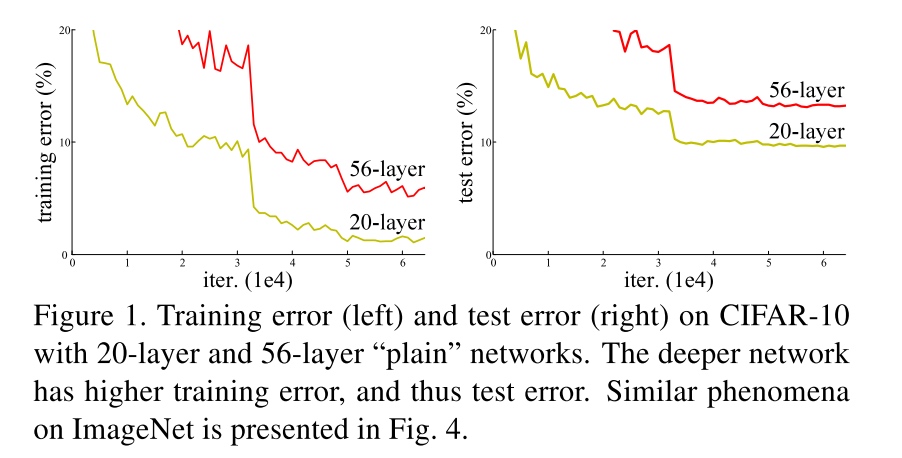
Figure 1 shows adding more layers to a suitably deep model leads to higher training error. This is unexpected because if the added layers are identity mapping, then a deeper model should produce no higher training error than its shallower counterpart.
ResNet
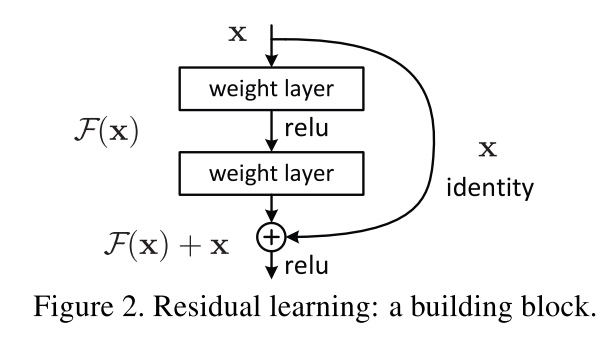
To solve the degradation problem of deeper network, the authors proposed ResNet. They explicitly let these layers fit a residual mapping. Formally, denoting the desired underlying mapping as $H(x)$, they let the stacked nonlinear layers fit another mapping of $F(x):= H(x)−x$. The original mapping is recast into $F(x)+x$.
Advantage:
- It is easier to optimize the residual mapping than to optimize the original, unreferenced mapping.
- To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.
- In real cases, it is unlikely that identity mappings are optimal, but our reformulation may help to precondition the problem. If the optimal function is closer to an identity mapping than to a zero mapping, it should be easier for the solver to find the perturbations with reference to an identity mapping, than to learn the function as a new one.
- Identity shortcut connections add neither extra parameter nor computational complexity.
- The deep residual nets can easily enjoy accuracy gains from greatly increased depth.
Network Architecture
-
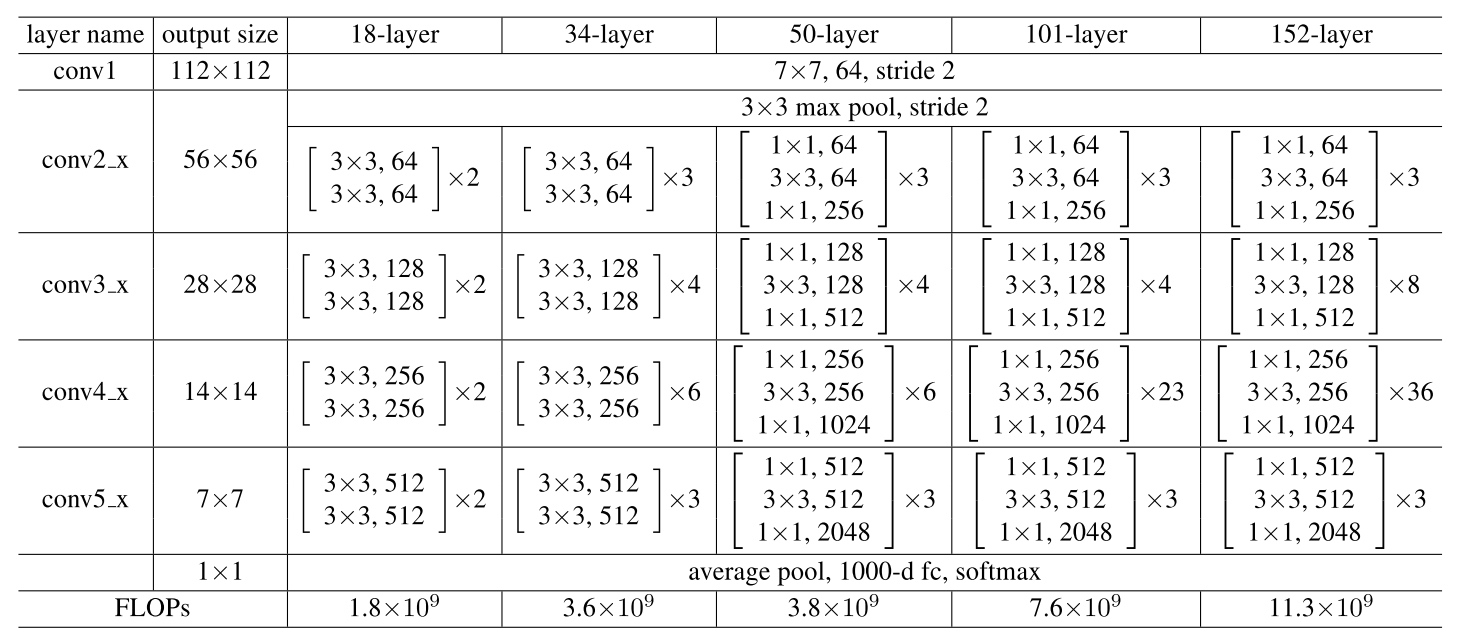
Network complexity: There is no fc-4096 in ResNet, which greatly reduce the complexity of ResNet. (Although the depth is significantly increased, the 152-layer ResNet (11.3 billion FLOPs) still has lower complexity than VGG-16/19 nets (15.3/19.6 bilion FLOPs).)
- Identity mapping and projection shortcuts:
- The identity shortcuts can be directly used when the input and output are of the same dimensions
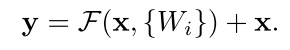
- When the dimensions increase, we consider two options: (A) The shortcut still performs identity mapping, with extra zero entries padded for increasing dimensions. This option introduces no extra parameter; (B) The projection shortcut is used to match dimensions (done by 1×1 convolutions).
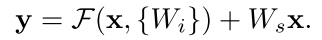
- The identity shortcuts can be directly used when the input and output are of the same dimensions
- Deeper Bottleneck Architecture
The three layers are 1×1, 3×3, and 1×1 convolutions, where the 1×1 layers are responsible for reducing and then increasing (restoring) dimensions, leaving the 3×3 layer a bottleneck with smaller input/output dimensions. (use option B for increasing dimensions.)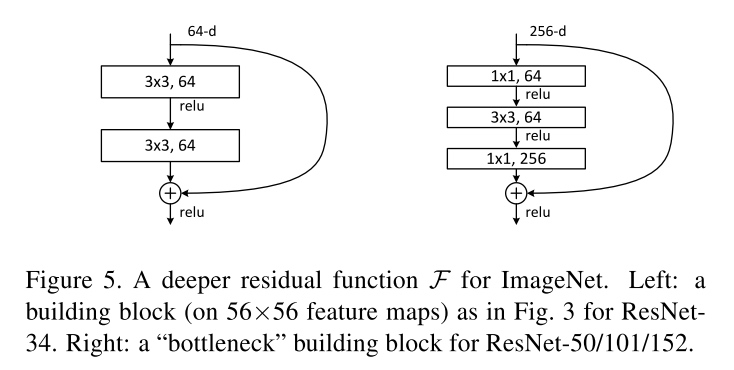
Detailed illustration
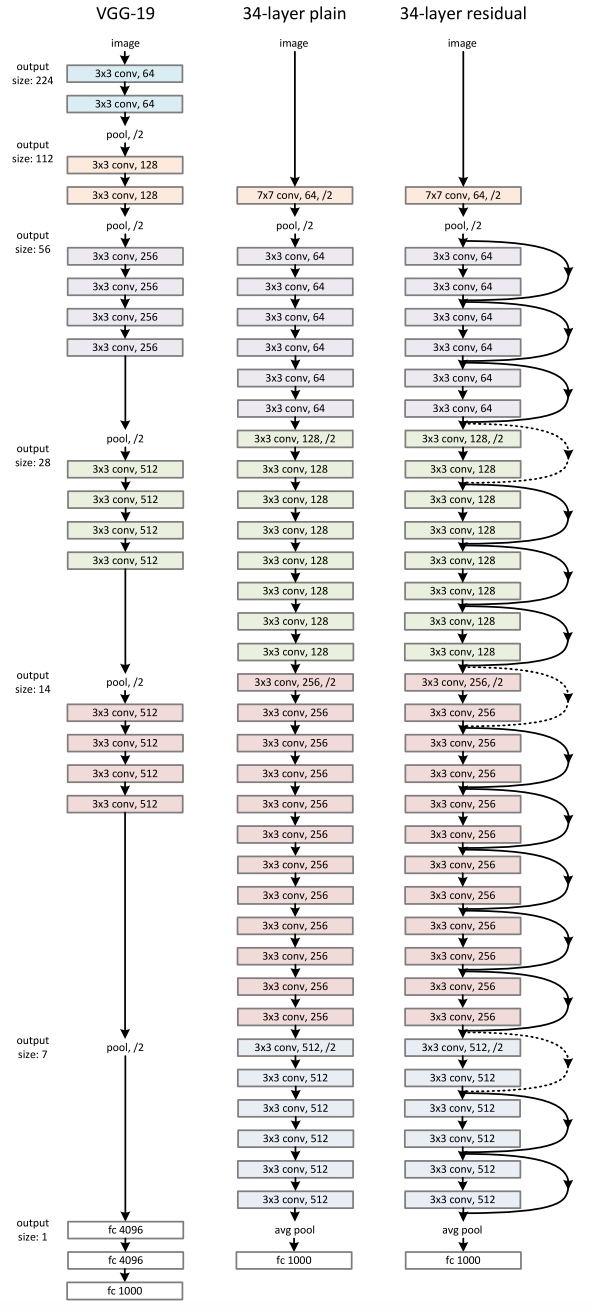
Experiments
Plain network and ResNet (zero padding for increasing dimension)
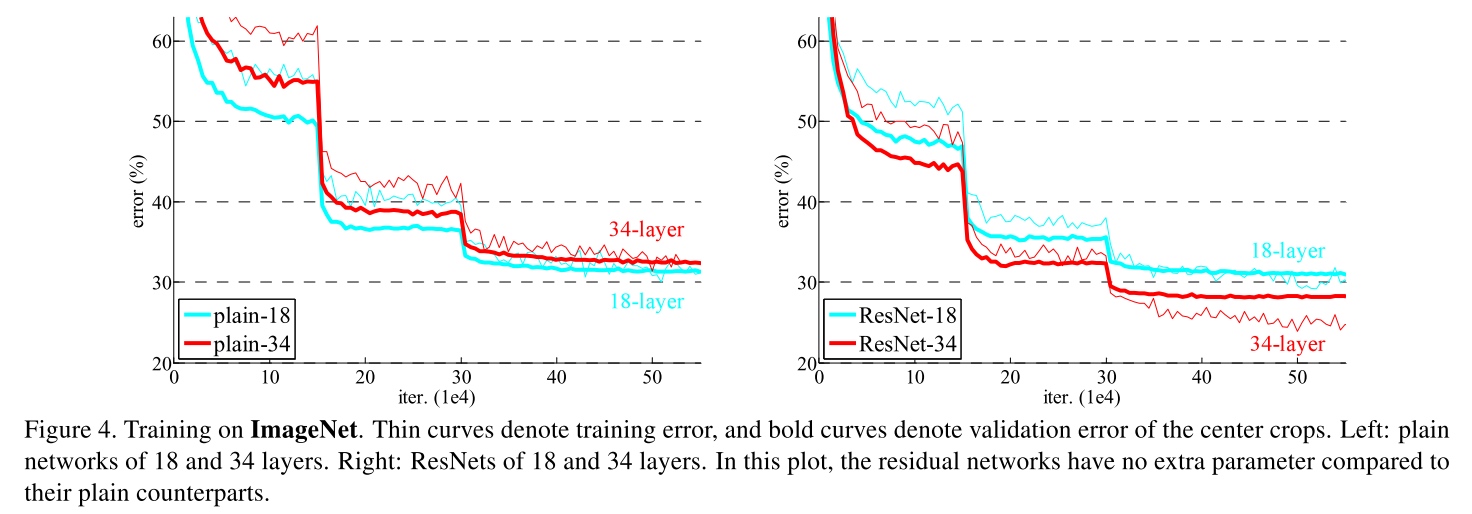
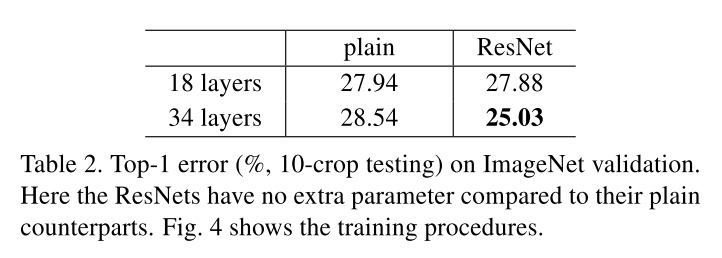
- The 34-layer ResNet exhibits considerably lower training error and is generalizable to the validation data. This indicates that the degradation problem is well addressed in this setting and we manage to obtain accuracy gains from increased depth.
- The effectiveness of residual learning on extremely deep systems: Compared to its plain counterpart, the 34-layer ResNet reduces the top-1 error by 3.5% (Table 2), resulting from the successfully reduced training error (Fig. 4 right vs. left).
- When the net is “not overly deep” (18 layers here), the 18-layer plain/residual nets are comparably accurate (Table 2), but the 18-layer ResNet converges faster.
Identity vs. Projection Shortcuts
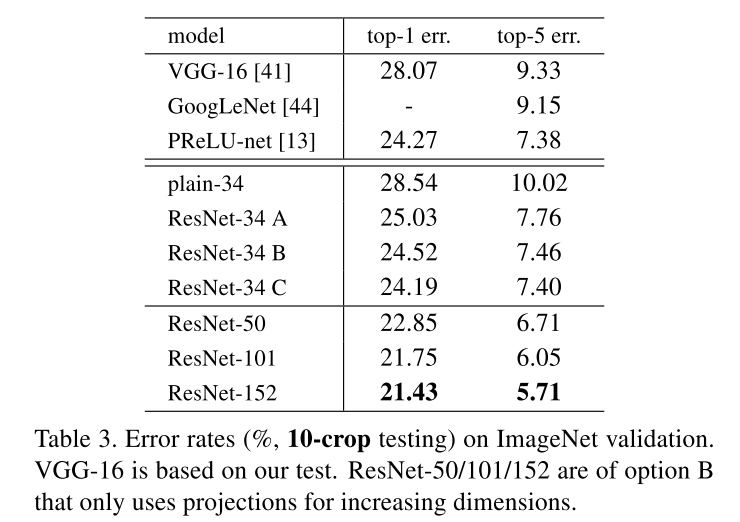 In Table 3 we compare three options:
In Table 3 we compare three options:
(A) zero-padding shortcuts are used for increasing dimensions, and all shortcuts are parameter-free
(B) projection shortcuts are used for increasing dimensions, and other shortcuts are identity
(C) all shortcuts are projections.
- B is slightly better than A.We argue that this is because the zero-padded dimensions in A indeed have no residual learning.
- C is marginally better than B, and we attribute this to the extra parameters introduced by many (thirteen) projection shortcuts.
- But the small differences among A/B/C indicate that projection shortcuts are not essential for addressing the degradation problem.
Deeper network
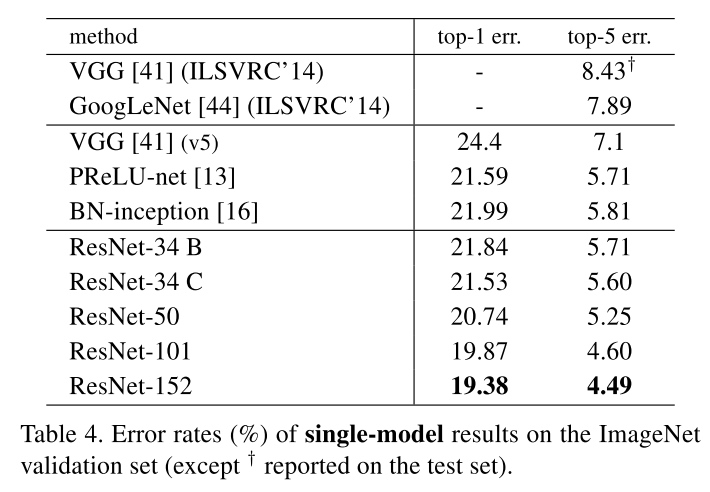 From Table 3 and 4, the 50/101/152-layer ResNets are more accurate than the 34-layer ones by considerable margins. We do not observe the degradation problem and thus en- joy significant accuracy gains from considerably increased depth.
From Table 3 and 4, the 50/101/152-layer ResNets are more accurate than the 34-layer ones by considerable margins. We do not observe the degradation problem and thus en- joy significant accuracy gains from considerably increased depth.
Analysis of layer reponses
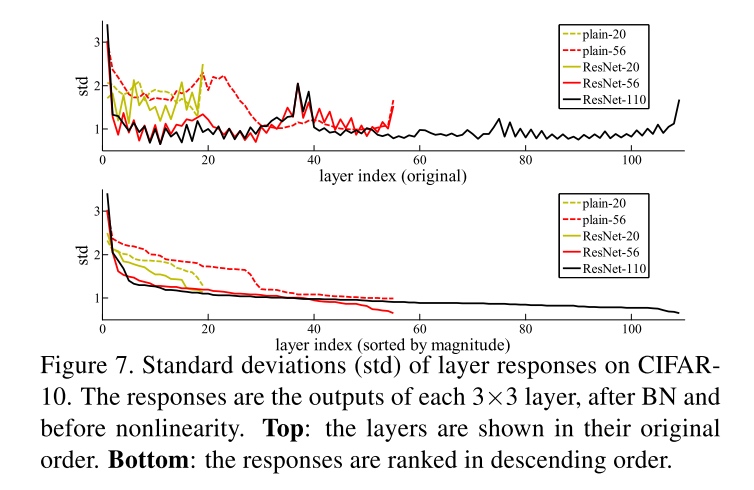
- ResNets have generally smaller responses than their plain counterparts. These results support our basic motivation that the residual functions might be generally closer to zero than the non-residual functions.
- The deeper ResNet has smaller magnitudes of responses, showing when there are more layers, an individual layer of ResNets tends to modify the signal less.
Exploring Over 1000 layers
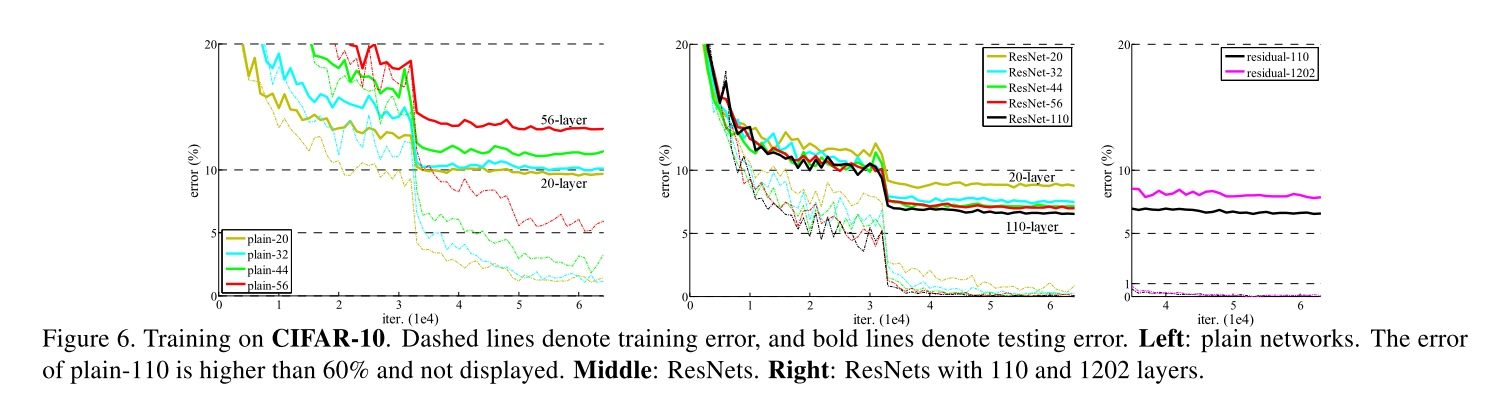 The testing result of this 1202-layer network is worse than that of our 110-layer network, although both have similar training error. We argue that this is because of overfitting. The 1202-layer network may be unnecessarily large (19.4M) for this small dataset. But combining with stronger regularization may improve results, which we will study in the future.
The testing result of this 1202-layer network is worse than that of our 110-layer network, although both have similar training error. We argue that this is because of overfitting. The 1202-layer network may be unnecessarily large (19.4M) for this small dataset. But combining with stronger regularization may improve results, which we will study in the future.